• Leap Year:
    • div by 4, if a 100 year, it should be div by 400
    • Ex: 1900 isn’t leap, despite being div by 4
  • Prime Number: https://hashdefine.netlify.app/maths
  • Sieve of Eratosthenes: Loop i -> 2 to sqrt(n), i++, loop j -> i*i to n, j+=i and untick elements
    • Time - O(n log logn)
  • Divisors: https://hashdefine.netlify.app/maths
  • Binary Exponentiation: https://cp-algorithms.com/algebra/binary-exp.html
    • derived from bitwise observation (iterative; fastest)
    • halving then squaring
    • squaring then halving (tail recursive)
    • for floating-point numbers and negative powers
  • Euclidean Algorithm: https://cp-algorithms.com/algebra/euclid-algorithm.html
    • for floating-point numbers
  • Fibonacci Numbers:
    • Recursion
    • Memoisation on Recursion (Top-Down DP)
    • Iterative Tabulation using Array (Bottom-Up DP)
    • Iterative that keeps track of only last two elements (space optimized)
    • Binet’s Formula (constant time mathematical)
  • Mod:
    • Smallest Integer Divisible by K: n = (n * 10 + 1) % k is like adding another 1 to the end of the number, and the % k keeps only the remainder so you never store the big number, just how it would behave when divided by k.

Divisors

Bulb Switcher - no. of odd/even divisors

Power of Three - prime factorization keep dividing by 3 until you get 1 or number not div by 3. Edge case is n = 0 where TLE happens, make n == 0 also false

Factorial Trailing Zeroes - we can calc factorial and keep dividing by 10 to get ans, we can also go to each number in range 1 - n and calc how many 2 and 5 factors are present, ans will be min(cntTwo, cntFive). This will cause overflow and TLE respectively.

  • Better way without calc factorial is through observation that in the factorial product there will be much more 2s than 5s because of all the even numbers in the range [1 - n], so we just need to count number of 5s
  • one 5 will be introduced into the product on every 5th number in the product i.e. n/5 is the number of zeroes (product) factorial n! will have, and we keep dividing the quotient until its less than 5 because numbers like 25 can add additional 5 e.g. 25 / 5 + 5 / 5 = 6 fives in factorization

Newton-Raphson Method

cp-algorithms topic page

  • sqrt(x - use binary search of Newton-Raphson method, both have O(log n) TC

Randomized Algorithms - Reservior Sampling

  • Random LL Node and Random Array Index - video link
    • Note that in random array problem, we skip elements not equal to target since probability should be equal among all target value elements (so reservior sampling works here too if we only keep count of the target value elements)
  • Shuffle the Array (such that all permutations are equally likely): video link
    • swap every element arr[i] with arr[rand(i, n-1)], i is inclusive
    • intuition: at every element prob of that element landing up at that position should be 1/n which isn’t possible if we don’t reduce the rand’s range

Geometry

Coordinate

Check If It Is a Straight Line - use slope m = y1 - y0 / x1 - x0, edge case = two points are always trivially on the same line. For the third point, slope should be equal to the first two points. Division by 0 will be an issue so check if (y2 - y1) * (x1 - x0) != (y1 - y0) * (x2 - x1) is true or false.

Triangle Inequality Theorem

Theorem: Sum of any two sides should be strictly greater than the third side inorder to form a triangle with them.
x + y > z
y + z > x
x + z > y

Largest Perimeter Triangle - we don’t need to find all triplets! this can be solved with a greedy approach, sort all sides, observation is that from the above three conditions, if x y z are sorted, we only need to check x + y > z and the other two conditions will be satisfied dude to sort property, track max on every valid condition

Distance Geometry

  • Euclidean Distance (diag is at sqrt(2) dist)
  • Manhattan (Taxicab) Distance (diag is at 2 dist)
  • Chebyshev Distance (diag is at 1 dist)

grid_diagram_showing_above_three_dist

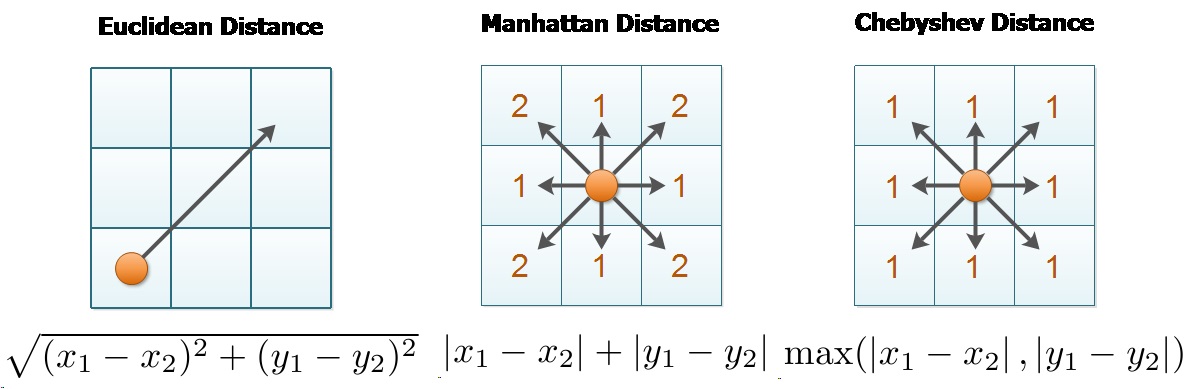
Usage in Chess: Rooks and Bishops use MD, Kings and Queens use CD

Minimum Time Visiting All Points - answer is sum of chebyshev’s distance (since diagonal dist is 1) between each pair of points

Combinatorics

Permutation: ways of arranging elements where ordering matters (distinct ordering of same content is counted multiple times)
nPr = n!/(n-r)!

Ex - ways of forming two letter words from string "ABC" will be 6 - "AB", "AC", "BA", "BC", "CA", "CB"

Re-arrangent/Factorial: ways of arranging all elements where order matters (generalized form of permuation where r = n)
nPn = n!

Ex - ways of rearranging string "ABC" will be 6 - "ABC", "ACB", "BAC", "BCA", "CAB", "CBA"

Combinations: ways of arranging elements where ordering doesn't matter
nPr = n!/(n-r)!*r!

Ex - ways of forming two letter words from string "ABC" will be just 3 - "AB", "AC", "BC". Since order doesn't matter, "AB" and "BA" are equivalent here.

Subsequences: they are nothing but Power Set (order doesn't matter; only content does in a set)
Each elements has two choices (pick/not-pick) = 2^n
Alternatively, all possible combination sizes = nCn + nCn-1 ... + nC0
Both of the above are equivalent!

Find count of all full length permutations of the string NUMBER where letter N occurs to the left of letter U: the count of occuring on right = count of occuring on left is symmetrical. So answer is n!/2. Another approach to this can be that pick any two places and they always remain fixed i.e. 6C2 and we permute the rest 4 places i.e. 4!, so answer is 6C2 * 4! that is equal to 6! / 2!.

Find count of all permutations of the string NUMBER where letter N occurs to the left of letter U and NU always occur together: treat NU as a single unit since they always occur together, hence answer becomes (n-1)!